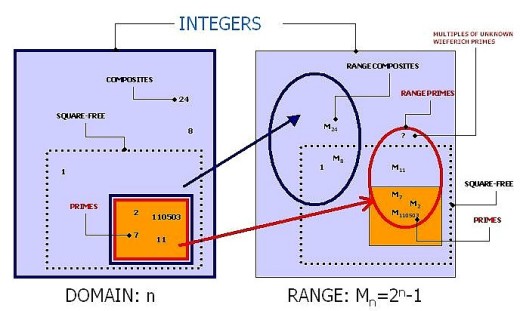
MERSENNE NUMBERS TREASURE MAP

17 02 2009

Mersenne Numbers Treasure Map

The Mersenne generating function splits the integer set in some subsets:

$\displaystyle \mathbb{N}\longrightarrow\mathbb{N}$

$\displaystyle f(n)\longrightarrow{2^{n}-1=M_n}$

1-INTEGERS PARTITION SET2-RANGE PARTITION SET

$\displaystyle f(0)=0$

$\displaystyle f(1)=1$

$\displaystyle f(Primes)\cap f(Composites) = \emptyset$

$\displaystyle f(Primes) \subset (Square Free \; \cup$ Composite factors of unknown Wieferich Primes $)$

$\displaystyle f(Primes) \cap Primes = \textrm{Prime Mersenne Numbers}$

$\displaystyle f(Composites)\subset Composites$

$\displaystyle f(Composites)\cap Primes=\emptyset$

$\displaystyle f(Square Free)\subset (Composites \cup \{ 1 \} )$

If $\displaystyle n=a*b$ is a composite number, then $\displaystyle M_{n}=M_{a*b}$ is also composite, because:
$\displaystyle M_{a*b}=2^{a*b}-1=(2^{a}-1)\cdot (1+2^a+2^{2a}+\dots+2^{(b-1)a})=$

$\displaystyle M_{a}*\sum_{i=1}^b{2^{(b-i)\cdot a}}$
And also if $\displaystyle d|n$ , and if $\displaystyle M_d$ , is not squarefree, then $M_n$ , can not be squarefree [8].

The only known Wieferich primes are 1093 and 3511, but they can not be prime factors of a Mersenne prime, see [6] and [7].

Note: See $\displaystyle \frac{M_{n^2}}{M_n}=\sum_{i=1}^n{2^{(n-i)\cdot n}}$ on link [5]

Archives:

[a]-021709-MERSENNE NUMBERS TREASURE MAP.ppt

References:[1]-A000225 The On-Line Encyclopedia of Integer Sequences!
[2]-A002808 The On-Line Encyclopedia of Integer Sequences!
[3]-A002808 The On-Line Encyclopedia of Integer Sequences!
[4]-A005117 The On-Line Encyclopedia of Integer Sequences!
[5]-A128889 The On-Line Encyclopedia of Integer Sequences!
[6]-Wieferich primes and Mersenne primes Miroslav Kures, Wieferich@Home – search for Wieferich prime.
[7]-Pacific J. Math. Volume 22, Number 3 (1967), 563-564 Henry G. Bray and Leroy J. Warren.
[8]-A049094 The On-Line Encyclopedia of Integer Sequences!

Actions

Information

Date : February 17, 2009
Categories : Mersenne

PSYCHEDELIC GEOMETRY